王思越

我们生活在一个永远不可能准确理解，但又不得不有个“合理”解释的世界中。

日志

关于我

hlwyjsh

博学之,审问之,慎思之,明辨之,笃行之。

文章分类

完全數與莫仙尼質數

2008-08-03 10:16:11| 分类：数学 | 标签： |举报 |字号大中小订阅

下载LOFTER 我的照片书 |

完全數與莫仙尼質數

張鎮華

完全數及數的個性

有一位數學老師問另一位音樂老師：「音樂裏只有七個音，你為什麼要花一生的時間去研究呢？」音樂老師遲疑了一下，反問道：「數學裏頭也只有十個數字，你又為何研究一輩子不清楚呢？」當然我們知道，音樂除了七音外，還有高低節奏等問題；數學除了數字以外，還有更抽象的符號，邏輯的架構。但是那位音樂老師的話，並不完全錯誤。我國古代用算盤計算數字，聰明的數學家製造出各種不同的魔方陣，今天，電子計算機快速算著各種巨大繁雜的數字。凡此種種，都足以表示，十個阿拉伯數字所排出來的東西多麼重要，人們對它充滿興趣。於是許多有用的，或這有趣的事物，遂應運而生。完全數 (Perfect Number) 就是一個古老而富有趣味的理論，以下我就針對這個題目，及有關的問題做一番討論。

數字和人一樣，也具有各種不同的個性。人有高矮、肥瘦、美醜和好壞之分。數字也類似地被賦予許性格。根據畢氏 (Pythagoras) 一派的說法，1 是萬物本源，1 生 2，2 生 3，類推可以得到無窮多數目；4 代表人的心靈，是一個最完滿的數；它們又把整數分成奇數和偶數兩類，易經上就有陰數和陽數的相似說法。此外，還有平方數、立方數、三角數、質數、合成數、完全數和互完數等不同的名詞。

G.H. Hardy（1887～1947）曾經寫了一則故事，描述印度數學家 Ramanujan（1887～1920），說明他能用各種幾乎辦不到的方法，記住各種數目的特性。有一次，Ramanujan 生病了，Littlewood 到 Putney 地方去看他，坐的計程車號碼是1729，他覺得這是一個難記住的數目，到了他那裡，就把這件事告訴他，他馬上反駁說：「那裡的話，1729是一個很有趣的數字，它是能用兩種方法表示為兩個數的立方和的最小數目。」這個故事把數字的個性說得最透徹 ¹ 。

完全數這個名詞很早就為人所熟悉，而且特別偏好。St. Augustine 曾說：「上帝在六天裏創造了宇宙萬物，因為六是一個完全數。」現在世界各國的曆制，都採用一星期七天，就是要工作六天，休息一天。

那麼你或許要問，完全數是什麼呢？完全數是指一個自然數且滿足以下的性質，即小於它的一切因數和等於這個數本身。

第一個完全數是

6 = 1+2+3

其次我們得到

28 = 1+2+4+7+14

再下去的完全數是

496 = 1+2+4+8+16+31+62+124+248

如果有人想用實驗的方法,再繼續找下去，必定不能得到很好的效果。畢氏學派的數學家 Nichomachus（BC 100），花了不少心血，到後來研究出「雖然善和美並不常在，但尚易尋求；至於醜和惡，卻比比皆是。」事實上，再下面兩個完全數是 8128 和 33550336，不見得容易尋求。這並不是說，一切已經絕望。試著運用觀察法尋求規律性，也許可以得到一些有用的東西。

$begin{displaymath}&10;begin{array}{l}&10;6 = 2 times 3 = 2^1(2^{1+1} -1) [3]&10;2...&10;...+1} -1) [3]&10;496 = 16 times 31 = 2^4(2^{4+1} -1)&10;end{array}end{displaymath}$

觀察上面三個式子，可以發現一個通性，或許具有 2ⁿ(2ⁿ⁺¹-1) 型式的數是完全數。但是當 n=3 時

2³ (2³⁺¹ -1) = 2³ * 15 = 120

這個數並不是完全數。因此，我們更進一步要注意 2ⁿ⁺¹ -1 的性質，當 n=1,2,4 時 2ⁿ⁺¹ -1 是質數，n=3 時 2ⁿ⁺¹-1 是合成數，關鍵就在這裏了。歐基里得（Euclid, 365?～275?B.C）在他的《原本》(Element) 中，證明了這個猜測。

完全數第一定理：
若 2ⁿ⁺¹ -1 是質數，則 2ⁿ(2ⁿ⁺¹ -1) 是完全數。

證：令 P 表示質數 2ⁿ⁺¹ -1 則 2ⁿ p 的因數（小於 2ⁿ p 本身的）有

$begin{displaymath}1,2,2^2, cdots , 2^n , 2p , cdots , 2^{n-1} p end{displaymath}$

它們的和

$begin{displaymath}&10;S = (1+2+ cdots cdots + 2^n) + p(1+2+cdots cdots + 2^{n-1})&10;end{displaymath}$

幾何級數

$begin{displaymath}1+2+2^2 + cdots cdots + 2^n = 2^{n+1} -1 end{displaymath}$

因此得

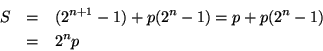
$begin{eqnarray*}&10;S &=& (2^{n+1} -1) + p(2^n -1) = p + p(2^n -1) &10;&=& 2^n p&10;end{eqnarray*}$

此數為完全數得證。

由第一定理得到的完全數都是偶數。是不是有奇完全數，這個問題沒有人知道，下面我們還會談到，至於是否還有其它的偶完全數，尤拉（Euler, 1707～1783）給我們一個完滿的答案。

完全數第二定理：
偶完全數必定呈 2ⁿ(2ⁿ⁺¹ -1 ) 的型式，其中 2ⁿ⁺¹ -1 為質數。

證：令偶完全數 $alpha = 2^n p$ ，其中 n 為自然數，p 為奇數。α 的一切因數和（包括 α 本身）為

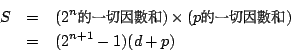
$begin{eqnarray*}&10;S &=& (2^n mbox{{fontfamily{cwM1}fontseries{m}selectfont ...&10;...ontseries{m}selectfont char 184}}) &10;&=& (2^{n+1} -1 )(d+p)&10;end{eqnarray*}$

其中 d 表示 p 的一切真因數和（不包括 p 本身）。

因為 $alpha$ 是完全數，因此

$begin{displaymath}&10;begin{array}{l}&10;alpha = S - alpha qquad mbox{{fontfami...&10;...2 alpha &10;(2^{n+1} -1)(d+p) = 2alpha = 2^{n+1}p&10;end{array}end{displaymath}$

化簡得到 p = (2ⁿ⁺¹ -1 )d

其中 2ⁿ⁺¹ -1 >1，而且 d 是 p 的因數，亦為真因數。

d 又是 p 的一切真因數的和，可見 p 為質數， d=1 。

$begin{displaymath}&10;P = (2^{n+1} -1 )d = 2^{n+1} -1 mbox{ {fontfamily{cwM1}fo...&10;...char 98}{fontfamily{cwM0}fontseries{m}selectfont char 1}}&10;end{displaymath}$

所以偶完全數 $alpha = 2^n ( 2^{n+1} -1)$ ，其中 2ⁿ⁺¹ -1 為質數。

莫仙尼 (Mersenne) 質數

尋找偶完全數的工作，到此變成，決定 2ⁿ -1 是否為質數的工作。尋求具有特別型式 M_p = 2^p -1 的質數，最早以法國數學家（Marin Mersenne, 1588～1648）算出最多，故我們用他名字稱呼此等質數，叫莫仙尼質數。

前面我們曾經說過 2³ (2⁴ -1) 並不是完全數。

現在可以運用第二定理說明，因為 2⁴ -1 = 15 不是莫仙尼質數，所以 2³(2⁴ -1) 不是偶完全數。

$begin{displaymath}&10;begin{array}{l}&10;M_2 = 2^2 -1 = 3 mbox{ {fontfamily{cwM1}...&10;...ontfamily{cwM1}fontseries{m}selectfont char 98}}&10;end{array}end{displaymath}$

觀察上面的例子，可以看出一個可能的通性，或許「p 為合成數時 M_p 為合成數，p 為質數時 M_p 為質數。」但是當我們試圖去證明這個敘述時，發現只有上半部才對。

定理 1
若 p 為合成數，則 M_p 為合成數。（若 M_p 為質數，則 p 為質數。）

證： p 為合成數，所以存在二個整數 a,b，使得 p = ab , 1 < a , b < p ,

$begin{eqnarray*}&10;M_p &=& 2^p -1 = 2^{ab} -1 &10;&=& (2^a -1 )[(2^a)^{b-1} + (2^a)^{b-2} + cdots + (2^a) +1 ]&10;end{eqnarray*}$

因為 $2^a -1 geq 2^2 -1 =3$ ，又

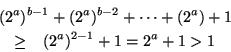
$begin{eqnarray*}&10;lefteqn{ (2^a)^{b-1} + (2^a)^{b-2} + cdots + (2^a) + 1 } &10;&geq& (2^a)^{2-1}+1 = 2^a +1 >1&10;\end{eqnarray*}$

所以 M_p 可以分解為兩個大於 1 的整數的積，必定為合成數。

如果 M_p 是質數，而 p 不是質數。

當 p=1 時，M_p =1 不是質數。

當 p 為合成數時，M_p 亦為合成數。

兩者均和已知 M_p 為質數矛盾，所以 p 為質數。

利用這個定理，當我們要尋找莫仙尼質數時，可以不必計算 p 為合成數時的情形。但是很不幸的是，這個定理的逆命題不成立，任你如何也證不出來，事實上，

$begin{displaymath}&10;begin{array}{l}&10;M_2 =3, ; M_3 = 7, ; M_5 = 31, ; M_7 = 127, [3]&10;M_{11} = 2047 = 23 times 89&10;end{array}end{displaymath}$

M₁₁ 是第一個和我們搗蛋的傢伙，於是我們的實驗工作，不得不繼續做下去，

$begin{displaymath}&10;M_{13} = 8191, ; M_{17} = 13,1071, ; M_{19} = 52,4287&10;end{displaymath}$

奇怪的是，得到的三個又全是質數。這些數目的位數越來越多，驗證工作也就顯得不容易。在初等數論裏有兩個定理可以幫助我們檢查一個數是不是質數。

: 定理2
大於 1 的整數必定有質因數。
: 定理3
如果整數 A 有合成數，必定有小於或等於 $sqrt{A}$ 的質因數。

定理 2 提供我們檢查一個數是否質數的方法：用小於 A 的一切質數去試驗，如果這些數都不是 A 的因數，那麼 A 就是質數了。定理 3 更方便，我們只要用小於 $sqrt{A}$ 的一切質數去試驗，就能決定 A 是不是質數。但是，即使使用這種方法，要算出 M₁₉ 是質數，已經十分不容易，於是又有下面的定理。

定理4
若 p 為質數，則 M_p 的質因數必呈 ap+1 的型式，其中 a 為正整數。

證：設 2^p -1 有一質因數 x=ap+b，其中 0<b<p（b 不可能 =0）
因 $2^p equiv 1 pmod{x}$
故

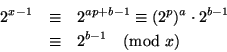
$begin{eqnarray*}&10;2^{x-1} & equiv & 2^{ap+b-1} equiv (2^p)^a cdot 2^{b-1} &10;& equiv & 2^{b-1} pmod{x}&10;end{eqnarray*}$

根據費瑪定理 ² $2^{x-1} equiv 1 pmod{x}$ ，所以 $2^{b-1} equiv 1 pmod{x}$
假設 b-1>0，因質數 p>b>b-1>0，所以 p 和 b-1 互質。
存在兩個正整數 α 和 β 使得，

$begin{displaymath}&10;alpha p = beta (b-1) +1 quad mbox{{fontfamily{cwM1}fontseries{m}selectfont char 67}} quad a(b-1) = beta p+1&10;end{displaymath}$

當 $alpha p = beta(b-1) +1$ 時，

$begin{displaymath}&10;2^{alpha p} equiv 2^{beta(b-1)+1} equiv (2^{b-1})^beta cdot 2 equiv 2 pmod{x}&10;end{displaymath}$

但

$begin{displaymath}&10;2^{alpha p} equiv (2^p)^alpha equiv 1 pmod{x} ;&10;Longr...&10;...us0.1pt{fontfamily{cwM7}fontseries{m}selectfont char 101}}&10;end{displaymath}$

同樣地，當 $a(b-1) = beta p + 1$ 時也矛盾。因此 b-1=0，即 b=1 本定理得證。

利用這個定理，檢驗工作又減輕不少。但是莫仙尼質數是呈幾何級數增大，當 p 越大， M_p 就越難檢驗。尤拉在1750年算出 M₁₉ 的次一莫仙尼質數 M₃₁，早期的尋找工作就算告一段落。1876年法國數學家洛克司 (Lucas) 用筆算出一個最大紀錄 M₁₂₇，這個數大達39位數，是人類用紙筆算出的12個莫仙尼數中之最大者。現在將這十二個質數列如下： 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127。

再下去的數越來越大，不是人類有限的精力所能擔當得了的。尤其莫仙尼質數的密度(density) 越來越小，要找到確實不容易。晚近電子計算機創造，計算能力逐日改良，使得這項工作得以繼續下去。最新的資料顯示，到目前為止，我們找到23個莫仙尼數，最大的一個是 M₁₁₂₁₃，居然高達3375位。

尾聲

完全數的尋找，比挖一顆鑽石還不容易。數學家都驕傲地以為，他們能夠用推理的方法，找出許多問題的答案，不像其他科學家，必須從實驗中，歸納出若干定理，但是遇到像偶完全數這樣的問題，就一籌莫展了。甚至，連偶完全數有限或者無限多個，還沒有人曉得，而且也不可能在短期間內曉得答案。

$begin{displaymath}&10;begin{array}{l}&10;a_1 = M_2 = 2^2 -1 =3 [3]&10;a_2 = M_3 = 2^...&10;...M_7 = 2^7 -1 =127 [3]&10;a_4 = M_{127} = 2^{127} -1&10;end{array}end{displaymath}$

洛克司能夠猜測，並且計算出 M₁₂₇ 是個質數，我們也可以做同樣的猜測： {a_n} 是莫仙尼質數所成的無窮數列，其中 a₁ = M₂, a_n+1 = M_{a_n}。猜測終究還是猜測，並不能告訴我們到底是否真確。如果是真的話，那麼莫仙尼質數，或者偶完全數就有無窮多個了。

除了偶完全數以外，是否還有奇完全數呢？這個問題到現在還沒解決。不過可以確定的是，如果奇完全數存在，那麼它一定很大。事實上，經過計算結果，如果有的話，奇完全數的階數必定大於 3。 [將一個自然數分解成質因數的積 p₁^a₁ p₂^a₂ … p_n^a_n，其中 p_i 為不同的質數，a_i 為正整數；其中的 n 姑且成為這個數的階 (order)。求完全數的工作，事實是也就是解 $2p_1^{a_1} p_2^{a_2} cdots p_n^{a_n}$ $= (sum_{i=0}^{a_1} p_1^i) (sum_{i=0}^{a_2} p_2^i) cdots&10;(sum_{i=0}^{a_n} p_1^n)$ 的工作。] 由計算機上得來更不好的消息。奇完全數的位數必定大於36。意思就是說，用紙和筆尋找奇完全數的工作，是不可能的。

评论这张

转发至微博

阅读(539)| 评论(0)

历史上的今天

this.p={  m:2,
              b:2,
              loftPermalink:'',
              id:'fks_084074083094086074082095082095081081088070087085085067',
              blogTitle:'完全數與莫仙尼質數',
              blogAbstract:'<DIV \><FONT face=\"標楷體\" \><FONT size=\"6\" \>完全數與莫仙尼質數</FONT\></FONT\></DIV\>  <P\><FONT face=\"標楷體\" size=\"5\" \>張鎮華</FONT\> </P\>  <P\>  <TABLE cellSpacing=\"0\" cellPadding=\"5\" width=\"480\" border=\"0\" \>  <TBODY\>  <TR\>  <TD width=\"480\" bgColor=\"#cedbff\" height=\"40\" \><FONT face=\"標楷體\" size=\"5\" \>完全數及數的個性</FONT\></TD\></TR\></TABLE\></P\>  <P\>有一位數學老師問另一位音樂老師：「音樂裏只有七個音，你為什麼要花一生的時間去研究呢？」音樂老師遲疑了一下，反問道：「數學裏頭也只有十個數字，你又為何研究一輩子不清楚呢？」當然我們知道，音樂除了七音外，還有高低節奏等問題；數學除了數字以外，還有更抽象的符號，邏輯的架構。但是那位音樂老師的話，並不完全錯誤。我國古代用算盤計算數字，聰明的數學家製造出各種不同的魔方陣，今天，電子計算機快速算著各種巨大繁雜的數字。凡此種種，都足以表示，十個阿拉伯數字所排出來的東西多麼重要，人們對它充滿興趣。於是許多有用的，或這有趣的事物，遂應運而生。完全數 (Perfect Number) 就是一個古老而富有趣味的理論，以下我就針對這個題目，及有關的問題做一番討論。   </P\><P\>  </P\><P\>數字和人一樣，也具有各種不同的個性。人有高矮、肥瘦、美醜和好壞之分。數字也類似地被賦予許性格。根據畢氏 (Pythagoras)</P\>',
              blogTag:'',
              blogUrl:'blog/static/57953330200873101611856',
              isPublished:1,
              istop:false,
              type:0,
              modifyTime:1316822853105,
              publishTime:1217729771856,
              permalink:'blog/static/57953330200873101611856',
              commentCount:0,
              mainCommentCount:0,
              recommendCount:0,
              bsrk:-100,
              publisherId:0,
              recomBlogHome:false,
              currentRecomBlog:false,
              attachmentsFileIds:[],
              vote:{},
              groupInfo:{},
              friendstatus:'none',
              followstatus:'unFollow',
              pubSucc:'',
              visitorProvince:'',
              visitorCity:'',
              visitorNewUser:false,
              postAddInfo:{},
              mset:'000',
              mcon:'',
              srk:-100,
              remindgoodnightblog:false,
              isBlackVisitor:false,
              isShowYodaoAd:false,
              hostIntro:'博学之,审问之,慎思之,明辨之,笃行之。\r\n',
              hmcon:'0',
              selfRecomBlogCount:'0',
              lofter_single:'<iframe width="140" height="560" style="overflow:hidden;" src="http://www.lofter.com/mailEntry.do?blogad=1&blog" frameBorder="0"></iframe>'
            }

{list a as x}
    {if !!x}
    <div class="iblock nbw-fce nbw-f40">
      <a class="fc03 noul" target="_blank" hidefocus="true" href="http://blog.163.com/${x.visitorName}/">
      {if x.visitorName==visitor.userName}
      <img alt="${x.visitorNickname|escape}" onerror="this.src=location.f40" class="cwd bdwa bdc0" src="${fn1(x.visitorName)}&r=${visitor.imageUpdateTime}"/>
      {else}
      <img alt="${x.visitorNickname|escape}" onerror="this.src=location.f40" class="cwd bdwa bdc0" src="${fn1(x.visitorName)}"/>
      {/if}
      </a>
      <div class="cwd vname thide">
        {if x.moveFrom=='wap'}
          <a class="noul pnt" target="_blank" href="http://blog.163.com/services/wapblog.html?frompersonalbloghome"><span title="来自网易手机博客" class="iblock wapIcon"> </span></a>
        {elseif x.moveFrom=='iphone'}
          <a class="noul pnt" target="_blank"><span title="来自iPhone客户端" class="iblock iphoneIcon"> </span></a>
        {elseif x.moveFrom=='android'}
          <a class="noul pnt" target="_blank"><span title="来自Android客户端" class="iblock androidIcon"> </span></a>
        {elseif x.moveFrom=='mobile'}
          <a class="noul pnt" target="_blank" href="http://blog.163.com/services/emsblog.html?frompersonalbloghome"><span title="来自网易短信写博" class="iblock wapIcon"> </span></a>
        {/if}
        <a class="fc03 m2a"  target="_blank" hidefocus="true" href="http://blog.163.com/${x.visitorName}/">
          ${fn(x.visitorNickname,8)|escape}
        </a>
      </div>
    </div>
    {/if}
    {/list}

<#--最新日志，群博日志--> <#--推荐日志-->

<p class="fc06">推荐过这篇日志的人：</p>
    <div>
      {list a as x}
      {if !!x}
      <div class="iblock nbw-fce nbw-f40">
        <a class="fc03 noul" target="_blank" hidefocus="true" href="http://blog.163.com/${x.recommenderName}/">
        <img alt="${x.recommenderNickname|escape}" onerror="this.src=location.f40" class="cwd bdwa bdc0" src="${fn1(x.recommenderName)}"/>
        </a>
        <div class="cwd thide">
          <a class="fc03 m2a" target="_blank" hidefocus="true" href="http://blog.163.com/${x.recommenderName}/">
            ${fn(x.recommenderNickname,6)|escape}
          </a>
        </div>
      </div>
      {/if}
      {/list}
    </div>
    {if !!b&&b.length>0}
    <p  class="fc06">他们还推荐了：</p>
    <ul>
    {list b as y}
      {if !!y}
        <li class="rrb"><span class="iblock">·</span><a class="fc03 m2a" target="_blank" href="http://blog.163.com/${y.recommendBlogPermalink}/?from=blog/static/57953330200873101611856">${y.recommendBlogTitle|escape}</a></li>
      {/if}
    {/list}
    </ul>
    {/if}

<#--引用记录--> <#--博主推荐--> <#--随机阅读--> <#--首页推荐--> <#--历史上的今天--> <#--被推荐日志--> <#--上一篇，下一篇--> <#-- 热度 -->

{list a as x}
    {if !!x}
    <div class="hotItem iblock nbw-fce nbw-f40">
      <a class="fc03 noul" target="_blank" hidefocus="true" href="http://blog.163.com/${x.publisherUsername}/">
      {if x.publisherUsername==visitor.userName}
      <img alt="${x.publisherNickname|escape}" onerror="this.src=location.f40" class="cwd bdwa bdc0" src="${fn1(x.publisherUsername)}&r=${visitor.imageUpdateTime}"/>
      {else}
      <img alt="${x.publisherNickname|escape}" onerror="this.src=location.f40" class="cwd bdwa bdc0" src="${fn1(x.publisherUsername)}"/>
      {/if}
      </a>
      <div class="cwd vname thide">
        <a class="fc03 m2a"  target="_blank" hidefocus="true" href="http://blog.163.com/${x.publisherUsername}/">
          ${fn(x.publisherNickname,8)|escape}
        </a>
      </div>
      <a class="f-myLikeIcons hottype {if x.type==1} js-liketype{elseif x.type==2} js-reblogtype{elseif x.type==3} js-sharetype{else}{/if}" target="_blank" hidefocus="true" href="http://blog.163.com/${x.publisherUsername}/"> </a>
    </div>
    {/if}
    {/list}

<#-- 网易新闻广告 --> <#--右边模块结构--> <#--评论模块结构--> <#--引用模块结构--> <#--博主发起的投票-->

页脚

我的照片书 - 手机博客 - 下载LOFTER APP - 订阅此博客

王思越

导航

日志

完全數與莫仙尼質數

历史上的今天

最近读者

热度

评论

页脚