凸函數、Jensen 不等式與 Legendre 變換
2008-08-03 10:31:38| 分类:
数学
| 标签:
|举报
|字号大中小 订阅
凸函數、Jensen 不等式與 Legendre 變換
林琦焜
凸函數的出現絕非偶然,在古典力學中的動能 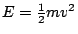 ,就是最自然直接的凸函數,其他如熵 (entropy)……等皆是,當然從幾何的角度而言就是拋物線。近代分析由於受凸分析研究所得之進展的影響,使得在非線性分析,非線性微分方程皆有長足之進展與突破,其中較重要的就是逐漸將非線性 (nonlinearity) 視為一個體,而非只是線性化 (linearization) 而已。凸函數是如此地美麗且重要,而一般教科書只是提個定義然後定理之後便是習題。對於這樣的數學,我們實在不滿足地無法忍受,畢竟數學要教導我們聰明並學習如何去思考。因此本文秉持此原則,將著重於幾何與物理直觀,並與一些相關聯的領域作一些對應,以思索在我們前面的那些數學巨人是如何思考問題。
,就是最自然直接的凸函數,其他如熵 (entropy)……等皆是,當然從幾何的角度而言就是拋物線。近代分析由於受凸分析研究所得之進展的影響,使得在非線性分析,非線性微分方程皆有長足之進展與突破,其中較重要的就是逐漸將非線性 (nonlinearity) 視為一個體,而非只是線性化 (linearization) 而已。凸函數是如此地美麗且重要,而一般教科書只是提個定義然後定理之後便是習題。對於這樣的數學,我們實在不滿足地無法忍受,畢竟數學要教導我們聰明並學習如何去思考。因此本文秉持此原則,將著重於幾何與物理直觀,並與一些相關聯的領域作一些對應,以思索在我們前面的那些數學巨人是如何思考問題。
我們從凸函數之定義開始
-
-
- 定義: f 為一定義在區間
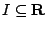 上之一實值函數 (real-valued function)
上之一實值函數 (real-valued function)
若對任意的 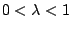 ,
,  ,f 滿足下式
,f 滿足下式
則稱 f 為一凸函數 (convex function)。
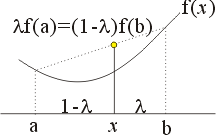
圖一 |
其幾何意義為連接 (a,f(a)),(b,f(b)) 兩點的弦,永遠在弧 y=f(x) 之上(圖一)。
利用分點公式我們可將(1)式表為下列之形式:
由(2)式可得
即
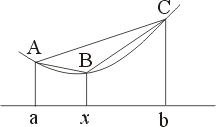
圖二 |
其幾何意義從圖形上之斜率可知。
我們的主要目的在於如何將(1)式推廣至一般情形。首先同時也是自然而然地(在數學上 2 與 n 是沒有差別的)將(1)式推廣至 n 個點 x1,…,xn。(可用歸納法)
其中 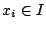 ,
, 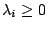 ,
, 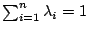 ,
,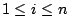 。有時候我們(有目的地)令
。有時候我們(有目的地)令
則(4)式可改寫為
這就是 Jensen 不等式之一形式。若取特殊的 pi,例如:
則(6)式可表為
典型的凸函數有底下的類型:
在尚未做進一步推廣前,Jensen 不等式最直接的應用就是幾何平均與算數平均之關係;讀者可自行練習
-
-
- 例題 1:(幾何-算數平均)試證
-
- (a)
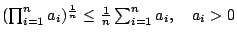
-
- (b)
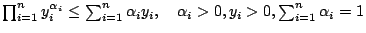
-
我們感興趣的問題是關於 Jensen 不等式(6)式或(7)式之幾何意義與物理意義,首先介紹質量中心:
假設平面上有 n 個點且它們皆有相同之質量,其位置向量為  ,
,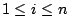 ,則質量中心之位置向量為
,則質量中心之位置向量為
或
這意思是從 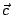 點到各點之向量彼此互相抵消。
點到各點之向量彼此互相抵消。
圖三 |
我們可以這麼想像:在每一點  為一釘有木樁而後用一條橡皮筋連接各點
為一釘有木樁而後用一條橡皮筋連接各點  。則如此可形成一多邊形 H(陰影區域)而這就是
。則如此可形成一多邊形 H(陰影區域)而這就是  的「凸包」(convex hull)。
的「凸包」(convex hull)。
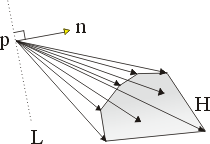
圖四 |
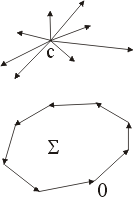
質量中心(9)式告訴我們的就是
這點可由圖形直觀而得。通過任意一點 P,P 在該集合之外部,我們可劃一直線 L 使得 H 及其所圍區域完全落在 L 之一邊。當然這些向量不可能互相抵消,因為它們在法向量  上均有正的分量。
上均有正的分量。 註:上面所談的這個概念其實就是泛函分析中 Banach Separation 定理之一雛形。
有了這個預備工作之後,我們回到原來的點:

圖五 |
令 K = {(x,f(x))} 為函數 f 之圖形 (graph),同時我們也連接兩端點 (x1,f(x1)),(xn,f(xn)),則由質量中心為
必定落在陰影區域 H 之內部,即
這就是(7)式,其意義為:質量中心 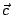 必定在圖形 K 之上方。而通過 (x1,f(x1)),(xn,f(xn)) 兩點之弦方程式為
必定在圖形 K 之上方。而通過 (x1,f(x1)),(xn,f(xn)) 兩點之弦方程式為
由圖形亦知
而且對所有 ![$x in I=[x_1,x_n]$](http://episte.math.ntu.edu.tw/articles/mm/mm_19_4_07/img34.gif) 下式成立
下式成立
這個不等式我們可視為比較定理(Comparison 定理)最簡單的形式,而這在微分方程理論中扮演著舉足輕重的角色。比較(7)與(12)式,各等式要成立其充分必要條件為質量中心 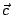 落在圖形 K 上,即
落在圖形 K 上,即
這相當於
如果將 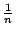 視為 xi 之機率分配(一致分配),則 Jensen 不等式(7),也可以用機率的角度來看
視為 xi 之機率分配(一致分配),則 Jensen 不等式(7),也可以用機率的角度來看
E 為期望值。 對於較一般的(6)式其意義仍是一樣的,即視 x1,…,xn 為 n 個點但其質量分別為 pi 而 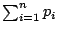 為其總質量,故有
為其總質量,故有
若視 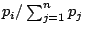 為點 xi 之機率分配,則上式可以期望值之形式表達出來,其形式與(15)式同。
為點 xi 之機率分配,則上式可以期望值之形式表達出來,其形式與(15)式同。 若仔細推敲,可知我們前面這些推導的過程中對維數 (dimension) 之依賴並不深,因此我們可自然地推廣至 n 維空間。例如設 z=f(x,y) 為一向上凹之曲面,則(7)式可推廣為
或用向量之形式 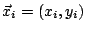
另一個方向的推廣則是想像粒子數目增加至無窮多個 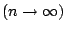 ,如此我們便可以從離散型過渡到連續型,表記如下:
,如此我們便可以從離散型過渡到連續型,表記如下:
這就是我們在數學上,尤其是分析學思想的過程而需要克服的問題──「收斂性」,即無窮級數或積分是否有意義(即是否收斂)。 在區間 [a,b] 我們可以取分割點
由(6)式知
將上式表為 Riemann 和之形式
再取極限  ,我們就有積分形式的 Jensen 不等式。
,我們就有積分形式的 Jensen 不等式。
-
- 定理(Jensen 不等式一)
- 若 p 滿足
 ,且 f 為一凸函數,則
,且 f 為一凸函數,則
更一般情形則將區間 [a,b] 代換為任意可測集合 A ( ![$[a,b] rightarrow A$](http://episte.math.ntu.edu.tw/articles/mm/mm_19_4_07/img54.gif) )
)
-
- 定理(Jensen 不等式二)
讀者若有機率或測度 (measure) 之概念,則可將 p 視為一密度函數,故有
-
- 定理(Jensen 不等式三)
作個簡單的習題,其實就是例題 1 之推廣
-
-
- 例題 2:
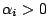 ,
, 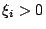 ,
,  ,試證
,試證
-
關於 Jensen 不等式之證明,最簡單直接的方法就是用支撐線 (supporting line) 之概念,而這方法在 F. Riesz 寫給 Hardy 的信中(1930年)就曾提過關於幾何-算術平均不等式的證明,就是利用底下之不等式
這就是支撐線 (supportingline) 之概念。
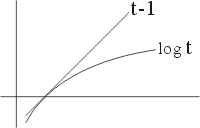
圖六 |
若 f 為區間 (0,1) 上的一個正的且可積函數,則由(24)式知 ( 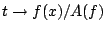 )
)
其中
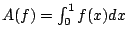
為
f 之算數平均,將上式積分一次得
由對數函數之性質知
或者表為
仿此精神我們證明 Jensen 不等式

圖七 |
由圖形知 y=f(r)+m(x-r),m=f'(r) 為凸函數 f(x) 之支撐線 (supporting line),即
現在取
r 為質量中心
而
x 則取為
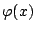
,則(26)式成為
兩邊同時乘
p 並積分得
但由
r 之選法知
故得
這就是 Jensen 不等式。
在尚未作進一步論述之前,我們不禁要對 F. Riesz 的想法獻上我們的敬意。所謂的「好數學」便是以簡單的方法來解決困難的問題,而不是學了很深的數學然後再說 "Trivial" 簡單、容易。這基本土是對數學的無知。另外一門好的數學就是其本身有「將來性」,而非解完一個問題便壽終正寢。我們要特別強調的是 Riesz 所提支撐線的概念,實際上就是 Legendre 變換之化身。不失一般性可設函數上通過原點,f(0)=0 因此通過 (r,f(r)) 之切線方程式(即支撐線)為
這式子告訴我們
(f'(r),f(r)-rf'(r)) 唯一決定點
(r,f(r)) 即這兩者之間可定義某種變換關係,而這就是我們要談的 Legendre 變換。在還沒有正式談 Legendre 變換之前,我們先看看(28)式之幾何意義。
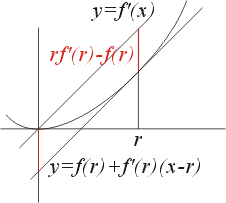
圖八 |
首先將切線平移為通過原點斜率為 f'(r) 之直線
因此
[rf'(r)-f(r)] 為直線
y=f'(r)x 之
y 截距,由圖形可知其實
即直線
y=f'(r)x 與曲線
y=f(x) 相割後垂直距離最寬者,而這就是 Legendre 變換。記為
直接由(31)式,即 Legendre 變換之定義可得的就是 Young's 不等式
一般我們所熟知的形式為(利用 Jensen 不等式)
有時候我們可略作變化
則(33)式可改寫為
這個技巧在分析尤其是偏微分方程中是常用的。上面這些探討主要是告訴讀者 Legendre 變換之本質是支撐線 (supporting line) 而實際上就是 Young's 不等式的另一形式。除此之外,支撐線的概念也提供我們重新定義凸函數之方法:
-
-
- 定義: f 為一定義在區間 [a,b] 之一連續函數,若對任意的點
![$xiin[a,b]$](http://episte.math.ntu.edu.tw/articles/mm/mm_19_4_07/img83.gif) 皆存在一相應之值
皆存在一相應之值  ,滿足下式
,滿足下式
則稱 f 為一凸函數。
這個定義可由 Taylor 展開式來看。f 在 ξ 點之 Taylor 展開式為
若
f 為一凸函數,則
f''>0 故有
因此通常(35)式中之 λ 是取
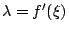
。
-
| |
任給兩個正數 a,b,其 p 階平均為
現在考慮函數 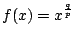 ,p<q,因為 ,p<q,因為 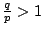 ,故 f 為一凸函數 (convex function)。因此由 Jensen 不等式知 ,故 f 為一凸函數 (convex function)。因此由 Jensen 不等式知
即
故
即如果將 Np 視為 p 之函數,則 Np 為 p 之增函數。同理可得積分形式的 p 階平均:
則
其中 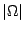 表示 Ω 之面積或體積。讀者若有實變函數論的觀念,則(39)式所表示的函數空間之關係為 表示 Ω 之面積或體積。讀者若有實變函數論的觀念,則(39)式所表示的函數空間之關係為
其中函數空間 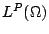 表示 p 次方後可積分之函數所形成之集合 表示 p 次方後可積分之函數所形成之集合
要特別叮嚀的是(40)式之關係,只有在 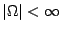 之條件下才成立,因為此時質量中心才有定義。 之條件下才成立,因為此時質量中心才有定義。 | | |
| |
凸函數在二維或更高維數的空間,例如複變函數,所對應的便是次調合函數 (subharmonic function)
對於此類函數具有非常重要地位的平均值不等式 (mean-value inequality) 為
BR (y) 表示以 y 為圓心,半徑為 R 之 n 維球, 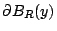 則表示其球面, 則表示其球面,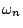 為 n 維單位球之體積。(43)式實際上就是 Jensen 不等式之一特例,但要特別叮嚀的是(41)式之積分區域務必要取均勻的球 BR (y) 或球面 為 n 維單位球之體積。(43)式實際上就是 Jensen 不等式之一特例,但要特別叮嚀的是(41)式之積分區域務必要取均勻的球 BR (y) 或球面 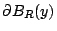 ,因為此時 y 是 BR (y) 或 ,因為此時 y 是 BR (y) 或 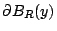 的質量中心。由(43)式可推得最大值原理 (maximum principle)。 的質量中心。由(43)式可推得最大值原理 (maximum principle)。 -
-
- 定理最大值原理(maximum principle):
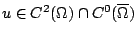 , , 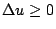 ,則 ,則
這定理告訴我們一個定義在有界區域 Ω 之次調合函數,其最大值必定發生在邊界 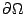 上。關於這件事實,我們亦可以凸函數之性質來想像。讀者可參考底下之圖形 上。關於這件事實,我們亦可以凸函數之性質來想像。讀者可參考底下之圖形

圖九 |
另外在偏微分方程中的 Laplace 方程 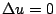 ,解之存在性證明方法中的 Perron 方法,也可由此角度來思考。 ,解之存在性證明方法中的 Perron 方法,也可由此角度來思考。

圖十 |
- D. Gilbarg and N.S. Trudinger, Elliptic Partial Differential Equations of Second Order, 2nd ed., Springer-Verlag (1983).
- G.H. Hardy, J.E. Littlewood and G. Pólya, Inequalities, Cambridge University Press, Cambridge (1952).
- Fritz John, Partial Differential Equations, 4th ed., Appl. Math. Sci., 1, Springer-Verlag (1982).
- T. Needham, A Visual Explanation of Jensen's Inequality, American Math. Monthly 100, 768-771 (1993).
|
评论这张
 转发至微博
转发至微博
 转发至微博
转发至微博
关闭
玩LOFTER,免费冲印20张照片,人人有奖!
我要抢>
<#--最新日志,群博日志-->
<#--推荐日志-->
<#--引用记录-->
<#--博主推荐-->
<#--随机阅读-->
<#--首页推荐-->
<#--历史上的今天-->
<#--被推荐日志-->
<#--上一篇,下一篇-->
<#-- 热度 -->
<#-- 网易新闻广告 -->
<#--右边模块结构-->
<#--评论模块结构-->
<#--引用模块结构-->
<#--博主发起的投票-->
![]() ,就是最自然直接的凸函數,其他如熵 (entropy)……等皆是,當然從幾何的角度而言就是拋物線。近代分析由於受凸分析研究所得之進展的影響,使得在非線性分析,非線性微分方程皆有長足之進展與突破,其中較重要的就是逐漸將非線性 (nonlinearity) 視為一個體,而非只是線性化 (linearization) 而已。凸函數是如此地美麗且重要,而一般教科書只是提個定義然後定理之後便是習題。對於這樣的數學,我們實在不滿足地無法忍受,畢竟數學要教導我們聰明並學習如何去思考。因此本文秉持此原則,將著重於幾何與物理直觀,並與一些相關聯的領域作一些對應,以思索在我們前面的那些數學巨人是如何思考問題。
,就是最自然直接的凸函數,其他如熵 (entropy)……等皆是,當然從幾何的角度而言就是拋物線。近代分析由於受凸分析研究所得之進展的影響,使得在非線性分析,非線性微分方程皆有長足之進展與突破,其中較重要的就是逐漸將非線性 (nonlinearity) 視為一個體,而非只是線性化 (linearization) 而已。凸函數是如此地美麗且重要,而一般教科書只是提個定義然後定理之後便是習題。對於這樣的數學,我們實在不滿足地無法忍受,畢竟數學要教導我們聰明並學習如何去思考。因此本文秉持此原則,將著重於幾何與物理直觀,並與一些相關聯的領域作一些對應,以思索在我們前面的那些數學巨人是如何思考問題。
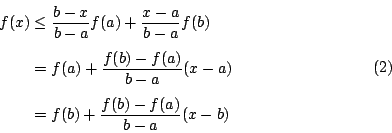


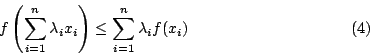
![]() ,
, ![]() ,
, ![]() ,
,![]() 。有時候我們(有目的地)令
。有時候我們(有目的地)令 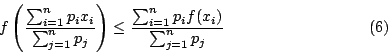
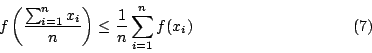
![]() ,
,![]() ,則質量中心之位置向量為
,則質量中心之位置向量為 
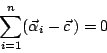

![]() 為一釘有木樁而後用一條橡皮筋連接各點
為一釘有木樁而後用一條橡皮筋連接各點 ![]() 。則如此可形成一多邊形 H(陰影區域)而這就是
。則如此可形成一多邊形 H(陰影區域)而這就是 ![]() 的「凸包」(convex hull)。
的「凸包」(convex hull)。 

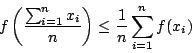


![]() 為其總質量,故有
為其總質量,故有 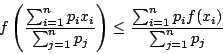
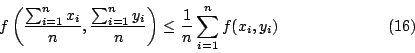

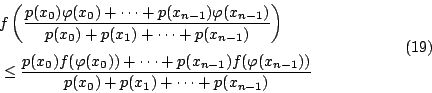

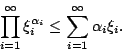

![]() )
) ![begin{displaymath}&10;begin{array}[t]{lcl}&10;{displaystyle exp big( int_0^1 lo...&10;...fontseries{m}selectfont char 204})}&10;end{array} eqno{(25)}&10;end{displaymath}](http://episte.math.ntu.edu.tw/articles/mm/mm_19_4_07/img67.gif)


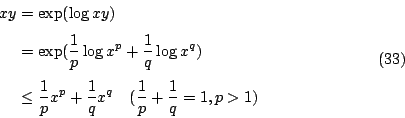
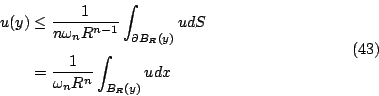
评论