蔡聰明
| 一、引言 |
Leibniz(1646~1716)在1714年發表一篇文章叫做 "Historia et origo calculi differentialis"(即《微分學的歷史與根源》),簡述他發明微積分的整個故事,開頭就這樣寫著:
對於值得稱頌的發明,了解其發明的真正根源與想法是很有用的,尤其是面對那些並非偶然的,而是經過深思熟慮而得的發明。展示發明的根源不光只是作為歷史來了解或是鼓舞其他人,更重要的是透過漂亮的發明實例,可以增進吾人發明的藝術,並且發明的方法也可公諸於世。當代最珍貴的發明之一就是一門新的數學分析叫做微分學的誕生。它的內涵已有足夠的解說,但是它的根源與動機卻少為人所知悉。它的發明幾乎已經有四十年的歷史了……。
然後 Leibniz 說出他發明微積分的根源就是差和分學。在他的一生當中,總是不厭其煩地解釋著這件得意的傑作。差和分與微積分之間的類推關係,恆是 Leibniz 思想的核心。從他的眼光看來,兩者在本質上是相同的。一方面,差和分對付的是離散的有限多個有限數;另一方面,微積分對付的是連續地無窮多個無窮小。因此,微積分若少了差和分就好像「Hamlet」劇本少了丹麥王子一樣。
| 二、生平簡述 |
Leibniz 在 1646 年誕生於德國的 Leipzig(萊比錫)。他父親是萊比錫大學的法學與道德哲學的教授。當他 6 歲時,父親就去世了。因此少年的 Leibniz 在學習的路途上幾乎沒有人指引他。這個小男孩所有的就是父親留給他的一個書的世界。一位聰慧而早熟的孩子,在約 8 歲時就自學拉丁文,12歲時開始學希臘文。這使得他沒有什麼困難就可以使用父親遺留下來的豐富的圖書館。泡在書海中,使他獲得了廣泛的古典作品之知識。他有能力閱讀幾乎所有的書,閱讀變成終身的興趣,這使他也讀了大量的壞書。後來 Leibniz 寫道:
當我還很年輕時,就開始認真思考各種問題。在15歲之前,我常常獨自一個人到森林中去散步,比較並且對照 Aristotle 與 Democritus 的學說。
Leibniz 在15歲時進入萊比錫大學就讀,選讀了宗教、哲學及初等算術,也聽了歐氏幾何的課,不過對幾何他並沒有投入。他試圖自己研讀 Descartes 的解析幾何學,但是對他來說似乎難一點。在17歲時,他提出一篇哲學論文,而得到學士學位。那年夏天他到 Jena 大學參加數學班,然後又回萊比錫大學攻讀邏輯、哲學與法律,次年就得到碩士學位。20歲寫出一篇優秀的組合學論文,但是由於他太年輕以致於萊比錫大學拒絕頒授給他博士學位。於是他轉到 Nuremberg 的 Altdorf 大學,並且在1667年(21歲)得到哲學博士學位。
完成學院工作後,他進入政治界,服務於 Mainz 政府。在1672年到1676年這段期間,由於外交任務的關係,他被派往法國的巴黎。在巴黎他遇到了當時歐洲大陸最有學問的 Huygens(1629~1695),激起他對數學的熱情,並且創造了微積分,使得在巴黎的四年成為他一生當中數學原創性的顛峰時期 (the prime age of creation),比美於 Newton 的1664~1666年這段時間。
Leibniz 在1680年給朋友的信裡,回憶他在1673年於巴黎遇到 Huygens 時所受到的啟發,他說:
那時我幾乎沒有多少時間研讀幾何。Huygens 給我一本他剛出版的關於單擺的著作。當時我對於 Descartes(笛卡兒)的解析幾何與求面積的無窮小論證法一無所知,我甚至不知道重心的定義。事實上,有一次跟 Huygens 討論時,我誤以為通過重心的任何直線必將面積平分為二,因為這對於正方形、圓形、橢圓形以及其它某些圖形顯然都成立。聽到我的話,Huygens 開始笑了起來,他告訴我沒有什麼東西能夠超越真理的。受到這個啟發,我非常興奮,在未徹底讀過歐氏幾何的情況下,我開始研讀高等幾何……。 Huygens 認為我是一個好的幾何學家,比我自估的還要好。他又交給我 Pascal 的著作,要我研讀。從中我學到了無窮小論證法、不可分割法以及重心的求法。
巴斯卡的著作給 Leibniz 打開了一個新世界,讓他靈光一閃,突然悟到了一些道理,逐漸地經營出他的微積分理論。
Leibniz 在1676年回到德國,於 Hanover 地方當政府的顧問與圖書館長,長達四十年之久。雖然他的職業是律師與外交官,但是他多才多藝,對各方面的學問都有極濃厚的興趣,並且以哲學家的身份聞名於世。由於他的極力鼓吹,柏林科學院才得以在1700年成立。
| 三、偉大的夢想 |
Leibniz 曾回憶說:
我小時候學邏輯,就開始養成對所學的東西作挖深的思考習慣。
他一生持久而不變的目標是追尋一種普遍的語言 (universal language) 與普遍的方法,使得可以統合地處理各式各樣的問題。研究 Leibniz 的學者 J.E. Hofmann(1899~1972)說:
Leibniz 熱情地,全心全力地收集與吸收能夠到手的所有知識,然後給予新的大綜合 (grand new synthesis),變成統一的整體。
Leibniz說:
我有滿腦子的主意 (ideas),如果能有更厲害的人深入去經營,將他們美妙的靈心與我的勞苦結合起來,會是很有用的。
他在1666年(當時20歲)寫出《組合學的藝術》(Art of combinatorics) 之論文。在前言中他預測這門新知識可以延拓應用到邏輯、歷史、倫理學、形上學,乃至整個科學。他又說:
假設我們可以用一些基本的字來表達人類的思想,因此可以想像有一系列的字,各代表了簡單的概念,那麼任何複雜的概念都可以用這些字組合起來。從而奇妙的「發明術」(the Art of invention) 就變成可能了:即所有可能的概念與命題都可以機械地產生。據此我們不但可以探討已知,而且也可以追尋未知,進一步從事更深刻的研究。
這個美麗的夢想在 Leibniz 心中盤據了一輩子。事實上,這只是古希臘哲學家 Dmocritus 所創立的原子論 (atomism) 的延伸與翻版。Democritus 主張宇宙的森羅萬象最終都可以化約成原子及其在空間中的運動、排列與組合,這是多麼美妙的想像。除了在物理學與化學上產生深遠的影響之外,在方法論 (methodology) 上,也開啟了分析與綜合的方法。追究事物的組成要素就是分析法,反過來由組成要素組合出事物就是綜合法。孫子在他的兵法中,說得更生動:
聲不過五,五聲之變,不可勝聽也;
色不過五,五色之變,不可勝觀也;
味不過五,五味之變,不可勝嘗也;
戰勢不過奇正,奇正之變,不可勝窮也;
奇正相生,如循環之無端,熟能窮之哉!
Leibniz 也夢想著要建立一套普遍的數學,他稱之為「Characteristica Universalis」,使得思想也可以化約成計算。他解釋說:
如果有了這樣的數學,那麼我們探討形上學與道德規範時,就可以如同幾何學與分析學之論證推理一般。兩個哲學家萬一發生意見衝突,他們的爭吵就不會嚴重過兩個會計員,這時只需拿起筆,平心靜氣地坐下來,然後互相說(必要的話可找個證人):讓我們計算一下。
Leibniz 對於發明術一直深感興趣,他說:
沒有什麼東西比看出發明的根源更重要,我認為這比發明出來的東西更有趣。
他計劃寫一本書來探討發明術,可惜從未實現。發明術也許只是人類永遠無法實現的一個夢想,好像是往昔的煉金術(發財夢)、煉丹術(長生夢)、永動機夢、煉預測未來術,以及近年來的煉基因術 (algeny) 一樣。人類需要有夢想,今日所證實的,也許就是過去的夢想。煉金術與煉丹術促成了化學的誕生,而煉發明術呢?它也產生了非常豐富的成果,例如認知科學 (cognitive science)、發明的心理學、人工智慧,大腦的思考機制之研究,Polya(1888~1985)關於數學的解題 (problem solving) 與猜測式推理 (plausible reasoning) 之精闢研究,以及近代科學哲學 (philosophy of science) 一改以往只重科學知識的「邏輯驗證」(the logic of justification) 而變成以「發現的理路」(the logic of discovery)為中心,專注於知識的成長與演化機制 (the growth and evolutional problem) 之探討,科學革命的結構之研究 (Thomas Kuhn)……等等。
Leibniz認為:
世界上的所有事情,都按數學的規律來發生。
這種深刻的「自然的數學觀」比美於 Galileo(1564~1642)的名言:「自然之書是用數學語言來書寫的」。據此,Leibniz 提倡世界的先定和諧論 (pre-estabilished harmony),並且論證這個世界是所有可能世界中最好的一個 (the best of all possible worlds),這是極值問題的一個應用。Einstein(1879~1955)說:
渴望窺探這個先定和諧的自然結構,是科學家不竭的毅力與恆心的泉源。
Leibniz 更有一顆敏銳的「妙悟靈心」,他早年就對這個世界感到驚奇而問道:
為什麼是存有而不是沒有呢?
(Why is there something instead of nothing?)
接著再問:
那裡存在的是什麼?
(What is there?)
對這些玄奧飄渺的問題深具興趣,正是「哲學心靈」的明證。古人提出了許多答案,例如原子論,畢氏學派的萬有皆數……等等。Leibniz 提出了單子論 (the theory of monads),單子是構成宇宙的至微單位,反映著大千世界,這恰是微積分中無窮小概念的抽象翻版。
在方法論 (methodology)上,Leibniz 強調充足理由原理 (the principle of sufficient reason):沒有東西是沒有理由的 (nothing is without reason);以及連續性原理 (the principle of continuity),他說:
沒有東西是突然發生的,自然不作飛躍,這是我的一大信條。
連續性原理有廣泛的解釋,例如從差和分連續化變成微積分就是一個好例子。另外,數學家 Cauchy(1789~1857)根據連續性原理宣稱,連續函數列的極限函數仍然是連續的,並且給出了一個錯誤的證明。後來才發現「均勻收斂」(uniform convergence) 必足以保證極限函數之連續性。
| 四、差和分學:從 Pascal 三角到 Leibniz 三角 |
在1672年春天,Leibniz 抵達巴黎,他的第一個成就是發現求和可以用求差來計算,即用減法可以求算加法。後來他曾描述他為何會想到差分以及差分的差分(即二階差分)等等的概念,並且強調差分扮演著他的所有數學思想的主角。在邏輯中,他徹底地分析真理,發現終究可化約成兩件事:定義與恆真語句 (indentical truths)。反過來,由恆真語句就可推導出豐碩的結果。他舉數列為例來展示:由 A=A 或 A-A=0 出發,可得
即 A - (A-B) - (B-C) - (C-D) - (D-E) - E = 0
令 A-B=K, B-C=L, C-D=M, D-E=N,
則得
亦即差之和等於第一項與最後一項之差。
換言之,給一個數列 v=(vk),考慮接續兩項之間的差
所成的數列 u=(uk),叫做(右)差分數列(還有左差分,同理可討論),那麼顯然有
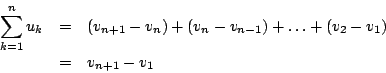
採用登山的解釋就很明白了:想像山路鋪成台階,每一階相對於地面的高度為 v1, v2, ![]() , vn+1,而階差高度為 u1, u2,
, vn+1,而階差高度為 u1, u2, ![]() , un,那麼從甲地登到乙地共昇高
, un,那麼從甲地登到乙地共昇高

另一方面這又等於 vn+1-v1,參見下圖 1。
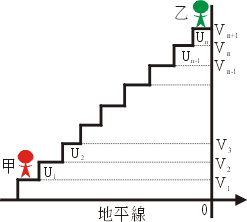 圖1 |

1+7+19+37+61=125-0=125,
7+19+37+61+91=216-1=215,
6+12+18+24+30=91-1=90,
12+18+24+30=91-7=84。
Leibniz 發現這個規律,覺得非常新奇、美妙,像小孩子玩積木一樣興奮不已。進一步,他研究 Pascal 三角(1654年,又叫算術三角)。Pascal 三角是作為開方、二項式展開、排列組合與機率之用,參見[2],Leibniz 卻從中玩索出差和分的道理。下面我們列出 Pascal 三角常見的三種排法:
(I)
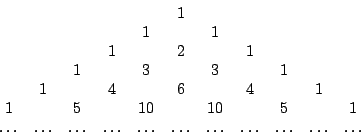
(II)

(III)
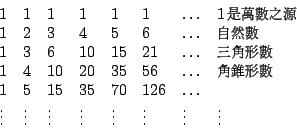
在(II)的排列法中,斜對角線上的數相加,所得到的數恰好構成費氏數列(Fibonacci sequence):
這個數列含有許多美妙的性質,我們不預備講述。
由(III)的排列法中,Leibniz 立即讀出許多關於行或列求和的結果,例如
同理
Leibniz 在巴黎遇到 Huygens 時,對 Huygens 描述他用求差來求和的結果,Huygens 立即建議他做下面富於挑戰性的問題。
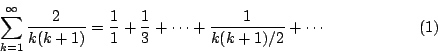
這個問題涉及無窮多項的相加,它源自計算某種賭局 (a game of chance) 的機率。
這個級數每一項的分母恰是畢氏學派「形數」(figurate numbers) 中的三角形數:
 |
因此,級數(1)就是三角形數的倒數之和。Leibniz 立即就求得這個和:因為
所以首 n 項之和為
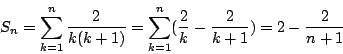
從而

我們在機率史的文獻上查不到 Huygens 的機率問題,不過我們倒有下面相關的例子:一個袋子裝有一個白球及一個黑球,從中任取一個球,若得白球就停止;若得黑球,則再填加一個黑球到袋中,變成兩黑一白,再任取一球,若得白球就停止;若又得黑球,則再添加一個黑球到袋中,變成三黑一白,如此繼續下去,那麼第一回合得白球的機率為 ![]() ,第二回合得白球的機率為
,第二回合得白球的機率為 ![]() ,第三回合得白球的機率為
,第三回合得白球的機率為 ![]() , … 等等,故終究得白球的機率為
, … 等等,故終究得白球的機率為
Leibniz 解決了 Huygens 問題後,進一步模仿 Pascal 三角,建構一個今日所謂的「調和三角」(harmonic triangle) 或 Leibniz 三角,一口氣解決了更多求無窮級數和的問題。
調和三角是這樣做成的:第一行排上調和數列,第二行依次排上第一行的前項減去後項之差,以後就按此要領做下去,結果如下:
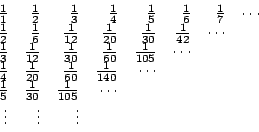
由此調和三角可以讀出
從而 Huygens 問題的答案是
另外我們也可以讀出
等等。將(2)式乘以 3 就得到角錐形數的倒數之和:
將(3)式乘以4就得到
同理也可得
Descartes 說得好:
由一個例子的考察,我們可以抽取出一條規律。
(From the consideration of an example we can form a rule.)
換言之,一個好的例子往往能夠反映出一般規律,即特殊孕育出普遍,或所謂的「一葉知秋」、「見微知著」的意思。我們由上述例子歸結出求和的共通模式 (pattern):

我們引入適當的概念與記號:
我們稱 ![]() 為數列 c 的(第一階)差分,Δ 為差分算子。
為數列 c 的(第一階)差分,Δ 為差分算子。 ![]() 叫做定和分(簡稱和分)。
叫做定和分(簡稱和分)。
因此,定理1 引出了兩個基本問題:
第一個問題很容易,在此從略。其次,利用(i),第二個問題原則上也不難。在 ![]() 中,我們稱 v 為 u 的反差分數列或不定和分。事實上,已知數列 u=(uk), k=1,2, … 定義一個新數列 b=(bn) 如下:
中,我們稱 v 為 u 的反差分數列或不定和分。事實上,已知數列 u=(uk), k=1,2, … 定義一個新數列 b=(bn) 如下:

則易驗知 b=(bn) 滿足
換言之,b=(bn) 就是 u=(un) 的一個不定和分。顯然,u 的不定和分不唯一,可以無窮多個(例如(5)式再加上任意常數都還是 u 的不定和分),但是任何兩個不定和分只差個常數。
對這一切作深入而有系統的研究就是差和分學的內容(包括差分方程)。差和分的學習對於微積分的了解非常有助益,因為兩者不過是離散與連續之間的類推與觀照而已。離散的差和分簡單明瞭,再連續化就得到了微積分。一般微積分教科書往往有如下的缺點:忽略差和分學,或類推與連續化處理得不好。
|
數列 u=(uk) 與函數 和分 (summation) 探究數列的求和
首先觀察到,和分可以解釋為下面圖 3 之柱狀圖的面積。
其次將函數 y = f(x) 離散化:作區間 [a, b] 的分割 考慮和分 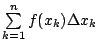 ,其幾何意義就是下圖 4 諸矩形所成的陰影面積,它是圖 2 的近似面積。 ,其幾何意義就是下圖 4 諸矩形所成的陰影面積,它是圖 2 的近似面積。
現在想像將 [a, b] 分割成無窮多段的無窮小段 dx(即微分),想成是差分 Leibniz 進一步把積分 就得到 一般而言, Leibniz 說: 像乘方與開方,和分與差分, |
如何求算積分 這是一個千古大難題。Archimedes 利用窮盡法 (the method of exhaustion),只會算出 Cavalieri(1598~1647)利用不可分割法或無窮小法 (the method of indivisible and infinitesimal) 求得 Fermat(1601~1665)利用動態窮盡法求得 這些都是個案解決,而且都算得相當辛苦。 Leibniz 有了微分與積分互逆的觀點,以及差和分根本定理,很快就看出「吾道一以貫之」的微積分根本定理,利用微分法普遍而系統地解決求積分的難題。這是微積分史,乃至人類文明史上的偉大時刻 (the great moment)。Leibniz 將他的發現在1693年發表。 考慮函數 由差和分根本定理知 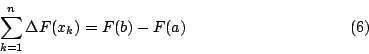 或者 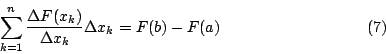 現在讓分割不斷加細,使每一小段都變成無窮小,將 Δ 改為 d, 從而,欲求 那麼就有 Eureka! Eureka! 我們自然就得到微積分裡最重要的一個結果:
Leibniz 創造優秀的記號,透過差和分根本定理,「直觀地」就看出了微積分根本定理。Leibniz 說: 值得注意的是,記號幫忙我們發現真理,並且以最令人驚奇的方式減輕了心靈的負荷。 Leibniz 一生對記號非常講究。數學家 Laplace(1749~1827)也說: 數學有一半是記號的戰爭。 我們要強調,記號的適當創造與掌握,是掌握數學的要訣。下面將 Leibniz 所創造的記號作個對照表:
在定理 3 中, 赫然出現了 首先讓我們來解釋它的幾何意義。 代表函數 y=F(x) 的圖形上,通過兩點 (xk,F(xk)) 與 (xk+1,F(xk+1)) 的割線斜率,參見圖 5。
無窮小化後的
因此,求積分 下面考慮 其中 dx 代表 x 的「無窮小」變化量, 由 F(x) 求出 如何求一個函數的導函數呢? 在做計算時,若採用無窮小論證法,就要記住無窮小詭譎的雙重性格:它不等於0,但是要多小就有多小。這樣看來,無窮小不是死的,而是活生生的小精靈。通常無窮小 dx 可正可負,即正無窮小與負無窮小,這種情形 dx 不等於 0,但其絕對值小於任意正實數。
如果你對「無窮小」感到「不自在」,那麼我們也可以採用極限論證法: 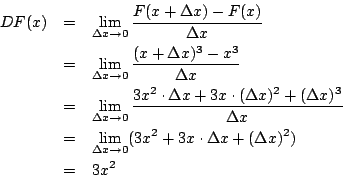 殊途同歸!在計算過程中,我們的論證是這樣的:由於 事實上,極限概念有直觀(良知良能)的一面,也有深奧的一面(
給一個數列 u,若數列 v 滿足 而稱 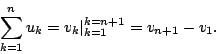 同理,由 我們就記為 而稱
總之,微積分就是利用極限或無窮小來建立微分與積分,再透過微分的逆向運算(由 f 求 d-1f)來求積分(面積、體積、表面積、曲線長、重心及里程等等),而微分的正向運算(由 F 求 dF 或 微分法是非常鋒利的兩面刃,是人類破天荒的成就。S. Bochner 說得好: 微分是一個偉大的概念,它不但是分析學而且也是人類認知活動中最具創意的概念。沒有它,就沒有速度或加速度或動量,也沒有密度或電荷或任何其它密度,沒有位勢函數的梯度,從而沒有物理學中的位勢概念,沒有波動方程;沒有力學,沒有物理,沒有科技,什麼都沒有 ([8], p.276)。
|
评论