王思越

我们生活在一个永远不可能准确理解，但又不得不有个“合理”解释的世界中。

日志

关于我

hlwyjsh

博学之,审问之,慎思之,明辨之,笃行之。

文章分类

拉普拉斯，費雪以及充分統計量的發現

2008-08-03 09:57:17| 分类：统计知识 | 标签： |举报 |字号大中小订阅

下载LOFTER 我的照片书 |

拉普拉斯，費雪以及充分統計量的發現

黃文濤

我們研究某一個母體，例如甲廠牌電視機的壽命，常設定有一個分佈函數，而這分佈函數就是在說明該廠牌出品的某一電視機其壽命（發生故障以前）大於某一段時間的機率。一般而言，這個分佈函數常帶有一個或數個未知參數。所以想瞭解該廠產品的壽命情況，勢必要設法去估計這些未知參數。由取樣（即記錄一些該廠出品電視機的壽命）來估計這些未知參數的問題，稱為統計估計問題，這在統計學上已成為一個專門研究的支系。那麼這些樣本值，如何處理，如何「過濾」，才會濾去不必要而留下那些真正與參數有關的資料，而且在處理或「過濾」過程中，不要遺漏了任何與參數有關的資訊。這就牽涉到充分統計量的概念。諸樣本值的(可測)函數而不帶任何未知量的稱為統計量。若諸隨機樣本的聯合機率函數，在某一統計量給定下之條件機率與某些參數（設稱為乙）無關時，則稱該統計量為這些乙參數之充分統計量。例如甲廠牌出品的電視機壽命一般視為服從指數分佈律，則其諸樣本的算術均數即為該廠牌「所有」產品的平均壽命（即該指數分佈的期望值）的充分統計量，而諸樣本和也是，所以充分統計量並非唯一。

英國著名統計學家 (R.A. Fisher) 在1920年的一篇論文中首先指出了充分統計量的概念，而這個「充分統計量」的名詞卻要到1922年的論文〈On the mathematical foundation of theoretical Statistics〉（論理論統計的數學基礎）才正式出現。實際上，《Nature》雜誌在1921年11月24日出版的摘要中首先出現。

英國天文學家艾靈頓 (A.S. Eddington) 在1914年出版的《星球運動和宇宙結構》一書中提到，對於估計一些觀測值的差誤，取其均值之差量的絕對值和 ( $sum_ivert x_i-overline{x}vert$ ) 比一般的差方和 ( $sum(x_i-overline{x})^2$ ) 來得恰當，但這卻與一般書上所寫的相反。為著檢驗他的主張，費雪開始作這兩形式的比較研究。他假設由均值為 m，變異數為 ( $sigma^2$ )（m, $sigma^2$ 均為未知參數）的常態分佈母體取 n 個樣本，設依次為 x₁,x₂,…,x_n，以 $overline{x}$ 表其樣本平均值。費雪研究了對於參數σ的兩種不同估計量，即 $sigma_1=frac{1}{n}sumvert x_i-xvert$ 與 $sigma_2=sqrt{frac{1}{n}sum(x_i-overline{x})^2}$ 。計算這兩個統計量的標準離散度（即變異數的平方根），發現當 n 大時， $sigma_1$ 之標準離散度比 $sigma_2$ 大了百分之十四，這與艾靈頓的說法不符（對於某一參數的估計統計量，其變異數愈小愈好，因為這表示其出現值的離散程度愈小）。費雪繼續又證明了基於 $sum_i(x_i-overline{x})^p$ 型式的估計量，當 p=2 時，其變異數為最小。其實，這除了費雪用漂亮的幾何方式證明之外，一點也沒有什麼新奇，因為早在1816年，高斯 (C. Gauss) 已發表了相同的結果。所幸費雪並不就此罷手，他進一步算了 n=4 時的 $sigma_1$ 與 $sigma_2$ 的聯合分佈函數（n 極大時， $sigma_1$ 與 $sigma_2$ 趨近於常態分佈，所以 n 小時，情況較複雜），而這時他發現了一個極有趣的現象：在 $sigma_2$ 給定某值之後， $sigma_1$ 之分佈居然與 σ 無關！而另一方面，在 $sigma_1$ 給定某值之下， $sigma_2$ 之分佈函數仍然含有參數 σ。這就說明了在尋找參數 σ 的資訊過程中，若先決定了 $sigma_1$ 值，我們仍然可以用 $sigma_2$ 來改進其估計值，但是，反過來，若先決定 $sigma_2$ ，那麼因為 $sigma_1$ 之分佈既與參數 σ 無關，那麼 $sigma_1$ 之實際值對於 σ 參數的資訊而言，實在一點價值也沒有。所以對於參數 σ 之資訊，若想由 $sigma_1$ 與 $sigma_2$ 得到，那麼它完全包括在 $sigma_2$ 之中。而且若有其他估計量 $sigma_3$ 用以代替 $sigma_1$ ，則同樣情況仍然出現。因此，對於參數 σ 之所有資訊，完全包括在 $sigma_2$ 之中。這些結果出現在1920年的論文中。

費雪同時也發覺到， $sigma_2$ 有這種性質與母體為常態分佈是互有關連的。當母體為雙指數分佈時，對於刻度參數 (scale parameter) 的估計，當 n 大時，費雪證明了 $sigma_1$ 比 $sigma_2$ 來得優越。在1922年的文章中，這種充分統計量的概念就完全清晰地刻畫了出來，他證明了所謂的「因子分解定理」(factorization theorem)，就是說，若諸樣本隨機變數的聯合密度函數可分解成某統計量的密度函數與某一完全不含參數的函數之乘積，那麼該統計量必是該參數的充分統計量，反之，也然。在以後的統計理論發展過程中，充分統計量扮演一個重要的角色。

故事到此還不能結束，因為比費雪早一百多年，大數學家拉普拉斯 (P.S. de　Laplace) 已作過了類似的研究。但這件事費雪似乎沒有注意到，因為在他的文章中，未提到拉氏的〈機率的解析理論第二增補篇〉(Deuxieme supplement a la Theorie Analytique des Probabilites)。這在1818年出版的增補篇裡，拉氏考慮了這樣一個問題（目前所謂的線性迴歸）：

有 n 個聯立方程式

$begin{displaymath}&10;p_iy-a_i+x_i=0 quad (i=1,2,cdots,n)&10;end{displaymath}$

其中 p_i,a_i 為已知，y 與 x_i 為未知，而 x_i 表觀測時的差誤，問題是如何估計 y 值。

在早期的著作中，他已討論過最小平方法，當時他稱之為「最有利方法」，而在這增補篇他討論另一個方法，稱為「情況法」(method of situation)。這是1757年由波斯柯維區 (Boscovich) 首先介紹的。其實這個方法在拉氏1799年出版的《天體力學》一書中已經提到。方法是這樣的，找出某 y 值使下面(1)式值為最小，

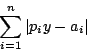$begin{displaymath}&10;sum^n_{i=1}vert p_iy-a_ivert&10;end{displaymath}$

(1)

拉式找出了這樣的解：
若

$begin{displaymath}&10;frac{a_1}{p_1}geqfrac{a_2}{p_2}geqcdotsgeqfrac{a_1}{p_1}&10;end{displaymath}$

而 r 滿足

$begin{displaymath}&10;p_1+p_2+cdots+p_{r-1}<p_r+cdots+p_n&10;end{displaymath}$

和

$begin{displaymath}&10;p_1 + p_2 + cdots + p_{r} > p_{r+1} + \cdots + p_n&10;\end{displaymath}$

時，那麼

$begin{displaymath}&10;y=frac{a_r}{p_r}&10;end{displaymath}$

(2)

必使(1)值最小。若以 y_{M_s} 表(2)式值，而以 y_{L_s} 表最小平方解，那麼

$begin{displaymath}&10;y_{L_s}=frac{sum_ip_ia_i}{sum_ip_i^2}&10;end{displaymath}$

拉氏假設觀測誤差 x_i 值依密度函數 $phi(x)$ 而變化。設 $phi(x)$ 在零點可兩次微分， $phi(x)>0$ ，且對稱於 0。他進一步導出了 (y_{M_s}-y) 之極限分佈，為均值為 0。變異數為

$begin{displaymath}&10;{(4phi^2(0)sum p_i^2)}^{-1}&10;end{displaymath}$

之常態分佈。他也導出了 y_{L_s} 之極限分佈，而且發覺，假如而且只有

$begin{displaymath}&10;(2phi(0))^2>(\int_{-\infty}^{\infty}x^2\phi(x)dx)^{-1} \qquad&10;\mbox{{\fontfamily{cwM1}\fontseries{m}\selectfont \char 118}}&10;\end{displaymath}$

y_{M_s} 比 y_{L_s} 優越（極限變異數較小）。他也注意到了 $phi(x)$ 為常態時，y_{L_s} 比 y_{M_s} 理想。事實上可以說，拉氏是第一位將兩種理想的估計量作比較的人，他也是第一位導出有序統計量的極限分佈的人（p_i=1,y_{M_s} 為中位數），他的方法可以由 $phi(x)$ 擴展到不對稱的情形，比起費雪的方法更一般化了。拉氏到此也未停止，他又進一步導出了該兩個估計值的聯合分佈，他的目的是如何經由這兩個估計量 y_{M_s} 與 y_{L_s} 作出一個新的更理想的估計量。他用特徵函數的反轉 (inversion) 來表 $xiequiv y_{M_s}$ 與 $xi ' equiv y_{M_s}$ 分佈，然後以無窮級數將積分展開，取 $nrightarrowinfty$ ，得到 $(xi,xi')$ 之密度分佈為

$begin{displaymath}&10;Ccdotexp {frac{-1}{4k'}xi^2q-2k'frac{[2xiphi(0)-frac{kxi'}{k'}]^2}{4(k'-2k^2)}q }&10;end{displaymath}$

此處 C 為常數．

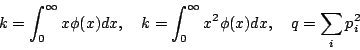
$begin{displaymath}k=int_0^{infty}xphi(x)dx,quad k=int_0^{infty}x^2phi(x)dx,quad q=sum_ip_i^2end{displaymath}$

顯然，這就是均值為

$begin{displaymath}&10;pmatrix{&10;0 cr&10;0 cr&10;}&10;end{displaymath}$

互變異矩陣為

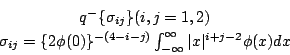
$begin{eqnarray*}&10;& q^-{sigma_{ij}}(i,j=1,2) & &10;& sigma_{ij}&10;= {2phi(0...&10;...{-(4-i-j)}int_{-infty}^{infty}vert xvert^{i+j-2}phi(x)dx &&10;end{eqnarray*}$

的二維常態分佈。利用這結果，他想找 α 使得

$begin{displaymath}&10;alpha y_{M_s}+(1-alpha)y_{L_s}&10;end{displaymath}$

之極限變異數為最小，他算出其值為

$begin{displaymath}&10;alpha=frac{{2phi(0)[2phi(0)-frac{k}{k'}]}}{frac{1}{2k'}-(frac{k}{k'})^2+[2phi(0)-frac{k}{k'}]^2}&10;end{displaymath}$

所以只要

$begin{displaymath}&10;2phi(0) > \frac{k}{k'} \; ,&10;\end{displaymath}$

那麼 y_{L_s} 還可以改良，只要減去

$begin{displaymath}&10;alpha(y_{L_s}-y_{M_s})&10;end{displaymath}$

當然，拉氏應該注意到只要 $phi(x)$ 與 e^-kx² 成正比，則

$begin{displaymath}&10;2phi(0)=frac{k}{k'} ; ,&10;end{displaymath}$

這就是說，只要 $phi(x)$ 為常態分佈，那麼 y_{L_s} 不只比 y_{M_s} 為優越，而且 y_{L_s} 再也不能改良。也就是說，不可能經由 y_{L_s} 與 y_{M_s} 的線性組合作出更優異的估計量。他也因此意識到 y_{M_s} 與 y_{L_s} 之線性組合都不可能經由 y_{L_s} 增加對於 y 值的資訊。可惜，在這個方向上，若拉氏再跨出半步，或者他也早就得出了類似充分統計量的概念來。他的出發點以及運算都比費雪的更一般化，但是費雪能夠在具體的情況中抽離出較抽象而富普遍性的概念來。若說這需要一百年的時間才能作到，誰會相信。但，平心而論，在拉氏的年代裡，數理統計還在嬰兒時期，最小平方法的發現也只有十三年的歷史，什麼點估計，也不過是一片模糊的瞭解而已，而對於常態分佈這麼一個特殊而重要的分佈，他的特殊性質也還未為一般人所熟悉。反觀費雪時代，已經由皮爾遜 (K. Pearson) 及其他人的刻意經營，立下基礎，而一些統計概念也更為清晰，這或許說明了在不同的背景下，得到了不同的結果。但無論如何，這兩位大家以富於創意與精於摸索的心靈，所作出的貢獻是不可磨滅的。

這樣一個統計學史上的故事，或許可以提供讀者一個印象，那就是對於一個具體的現象，或者數個看似無關的的個別現象，能夠抽離出或歸納出一個新的，更高層面的概念或體系，這種敏銳的洞察和歸納能力在科學工作上甚或思疇範圍內是及其重要且必須的，將原來的層面提升到更高的不同性質的層面，才在事物發展過程中具有進步的意義，然而這種提昇不可能憑空而來的，正如前所敘，經過皮爾遜等人工作的累積，才有費雪作抽象的提昇。拉氏在這方面的工作雖然展示了他那超越常人的蓬勃的創力才華，但是在向更高層面的突破跨越上，他並沒有成功，然而他的工作並非白費，他立下了很好的起點，導引了後人的提昇。

评论这张

转发至微博

阅读(535)| 评论(0)

历史上的今天

this.p={  m:2,
              b:2,
              loftPermalink:'',
              id:'fks_084074083094086074087095082095081081088070087085085067',
              blogTitle:'拉普拉斯，費雪以及充分統計量的發現',
              blogAbstract:'<DIV \><FONT face=標楷體\><FONT size=6\>拉普拉斯，費雪以及充分統計量的發現</FONT\></FONT\></DIV\>\r\n<P\><FONT face=標楷體 size=5\>黃文濤</FONT\> </P\>\r\n<P\>我們研究某一個母體，例如甲廠牌電視機的壽命，常設定有一個分佈函數，而這分佈函數就是在說明該廠牌出品的某一電視機其壽命（發生故障以前）大於某一段時間的機率。一般而言，這個分佈函數常帶有一個或數個未知參數。所以想瞭解該廠產品的壽命情況，勢必要設法去估計這些未知參數。由取樣（即記錄一些該廠出品電視機的壽命）來估計這些未知參數的問題，稱為<SPAN \>統計估計問題</SPAN\>，這在統計學上已成為一個專門研究的支系。那麼這些樣本值，如何處理，如何「過濾」，才會濾去不必要而留下那些真正與參數有關的資料，而且在處理或「過濾」過程中，不要遺漏了任何與參數有關的資訊。這就牽涉到充分統計量的概念。諸樣本值的(可測)函數而不帶任何未知量的稱為</P\>',
              blogTag:'',
              blogUrl:'blog/static/5795333020087395717405',
              isPublished:1,
              istop:false,
              type:0,
              modifyTime:0,
              publishTime:1217728637405,
              permalink:'blog/static/5795333020087395717405',
              commentCount:0,
              mainCommentCount:0,
              recommendCount:0,
              bsrk:-100,
              publisherId:0,
              recomBlogHome:false,
              currentRecomBlog:false,
              attachmentsFileIds:[],
              vote:{},
              groupInfo:{},
              friendstatus:'none',
              followstatus:'unFollow',
              pubSucc:'',
              visitorProvince:'',
              visitorCity:'',
              visitorNewUser:false,
              postAddInfo:{},
              mset:'000',
              mcon:'',
              srk:-100,
              remindgoodnightblog:false,
              isBlackVisitor:false,
              isShowYodaoAd:false,
              hostIntro:'博学之,审问之,慎思之,明辨之,笃行之。\r\n',
              hmcon:'0',
              selfRecomBlogCount:'0',
              lofter_single:'<iframe width="140" height="560" style="overflow:hidden;" src="http://www.lofter.com/mailEntry.do?blogad=1&blog" frameBorder="0"></iframe>'
            }

{list a as x}
    {if !!x}
    <div class="iblock nbw-fce nbw-f40">
      <a class="fc03 noul" target="_blank" hidefocus="true" href="http://blog.163.com/${x.visitorName}/">
      {if x.visitorName==visitor.userName}
      <img alt="${x.visitorNickname|escape}" onerror="this.src=location.f40" class="cwd bdwa bdc0" src="${fn1(x.visitorName)}&r=${visitor.imageUpdateTime}"/>
      {else}
      <img alt="${x.visitorNickname|escape}" onerror="this.src=location.f40" class="cwd bdwa bdc0" src="${fn1(x.visitorName)}"/>
      {/if}
      </a>
      <div class="cwd vname thide">
        {if x.moveFrom=='wap'}
          <a class="noul pnt" target="_blank" href="http://blog.163.com/services/wapblog.html?frompersonalbloghome"><span title="来自网易手机博客" class="iblock wapIcon"> </span></a>
        {elseif x.moveFrom=='iphone'}
          <a class="noul pnt" target="_blank"><span title="来自iPhone客户端" class="iblock iphoneIcon"> </span></a>
        {elseif x.moveFrom=='android'}
          <a class="noul pnt" target="_blank"><span title="来自Android客户端" class="iblock androidIcon"> </span></a>
        {elseif x.moveFrom=='mobile'}
          <a class="noul pnt" target="_blank" href="http://blog.163.com/services/emsblog.html?frompersonalbloghome"><span title="来自网易短信写博" class="iblock wapIcon"> </span></a>
        {/if}
        <a class="fc03 m2a"  target="_blank" hidefocus="true" href="http://blog.163.com/${x.visitorName}/">
          ${fn(x.visitorNickname,8)|escape}
        </a>
      </div>
    </div>
    {/if}
    {/list}

<#--最新日志，群博日志--> <#--推荐日志-->

<p class="fc06">推荐过这篇日志的人：</p>
    <div>
      {list a as x}
      {if !!x}
      <div class="iblock nbw-fce nbw-f40">
        <a class="fc03 noul" target="_blank" hidefocus="true" href="http://blog.163.com/${x.recommenderName}/">
        <img alt="${x.recommenderNickname|escape}" onerror="this.src=location.f40" class="cwd bdwa bdc0" src="${fn1(x.recommenderName)}"/>
        </a>
        <div class="cwd thide">
          <a class="fc03 m2a" target="_blank" hidefocus="true" href="http://blog.163.com/${x.recommenderName}/">
            ${fn(x.recommenderNickname,6)|escape}
          </a>
        </div>
      </div>
      {/if}
      {/list}
    </div>
    {if !!b&&b.length>0}
    <p  class="fc06">他们还推荐了：</p>
    <ul>
    {list b as y}
      {if !!y}
        <li class="rrb"><span class="iblock">·</span><a class="fc03 m2a" target="_blank" href="http://blog.163.com/${y.recommendBlogPermalink}/?from=blog/static/5795333020087395717405">${y.recommendBlogTitle|escape}</a></li>
      {/if}
    {/list}
    </ul>
    {/if}

<#--引用记录--> <#--博主推荐--> <#--随机阅读--> <#--首页推荐--> <#--历史上的今天--> <#--被推荐日志--> <#--上一篇，下一篇--> <#-- 热度 -->

{list a as x}
    {if !!x}
    <div class="hotItem iblock nbw-fce nbw-f40">
      <a class="fc03 noul" target="_blank" hidefocus="true" href="http://blog.163.com/${x.publisherUsername}/">
      {if x.publisherUsername==visitor.userName}
      <img alt="${x.publisherNickname|escape}" onerror="this.src=location.f40" class="cwd bdwa bdc0" src="${fn1(x.publisherUsername)}&r=${visitor.imageUpdateTime}"/>
      {else}
      <img alt="${x.publisherNickname|escape}" onerror="this.src=location.f40" class="cwd bdwa bdc0" src="${fn1(x.publisherUsername)}"/>
      {/if}
      </a>
      <div class="cwd vname thide">
        <a class="fc03 m2a"  target="_blank" hidefocus="true" href="http://blog.163.com/${x.publisherUsername}/">
          ${fn(x.publisherNickname,8)|escape}
        </a>
      </div>
      <a class="f-myLikeIcons hottype {if x.type==1} js-liketype{elseif x.type==2} js-reblogtype{elseif x.type==3} js-sharetype{else}{/if}" target="_blank" hidefocus="true" href="http://blog.163.com/${x.publisherUsername}/"> </a>
    </div>
    {/if}
    {/list}

<#-- 网易新闻广告 --> <#--右边模块结构--> <#--评论模块结构--> <#--引用模块结构--> <#--博主发起的投票-->

页脚

我的照片书 - 手机博客 - 下载LOFTER APP - 订阅此博客

王思越

导航

日志

拉普拉斯，費雪以及充分統計量的發現

历史上的今天

最近读者

热度

评论

页脚